Ensembles statistiques

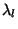Les contraintes physiques extérieures sur le système étudié sont appliquées par le biais de multiplicateurs de Lagrange. L'observable $A_{l}$ (variable extensive) associée à $\lambda_{l}$ (paramètre intensif) se retrouve alors distribuée dans un intervalle. Par exemple le multiplicateur de Lagrange associé au volume est la pression, celui associé au nombre de particules le potentiel chimique ou encore celui associé à l'énergie la température. Pour toute observable nous pouvons définir un paramètre de Lagrange (conjugué canonique) qui permettra d'obtenir la distribution de cette observable à l'équilibre de Gibbs, c'est à dire celle maximisant l'entropie statistique sous contraintes. Cette méthode permet de traiter de façon équiprobable l'information dont on ne dispose pas, le seul biais introduit étant précisément l'information pertinente.
Un algorithme Monte-Carlo de type Metropolis [2] permet d'échantilloner différents ensembles statistiques afin d'obtenir les distributions statistiques de microétats satisfaisant les contraintes. Il est possible d'ajouter à ces contraintes des lois de conservations (distribution de Dirac de l'observable conservée). Nous considérerons les ensembles grand-canonique dans lequel le potentiel chimique et la température sont fixés (ie. nombre de particules et energie définis en valeur moyenne) ainsi que l'ensemble canonique où la masse est fixée et l'énergie est définie en valeur moyenne. Les distributions de probabilité pour chaque ensemble statistique sont rappelées dans le tableau 1.