Bimodalité

Une fois les distributions statistiques de microétats obtenues, les projections de la densité d'état sur des directions d'observation jugées pertinentes permet d'étudier la physique associée au système.

F. Gulminelli et P. Chomaz ont proposé [3] d'utiliser la topologie de la distribution des évènements dans l'espace d'observation pour signer la transition de phase pour les systèmes de taille finie. Dans la zone de coéxistence de phase une bimodalité (deux maxima) dans la distribution de probabilité d'une observable permet d'identifier sans ambigüité chacune des phases; cette observable joue alors le rôle d'un paramètres d'ordre. La projection de la densité de probabilité dans des espaces d'observation pertinents permet d'identifier l'appartenance des évènements à chacune de ces phases.

La densité de matière est le paramètre d'ordre naturel de la transition de phase liquide-gaz à la limite thermodynamique. Il est toutefois possible de trouver d'autres paramètres d'ordre corrélés à la densité; en particulier on peut s'attendre à ce que la taille du plus gros des fragments ($A_{big}$) puisse servir de paramètre d'ordre.

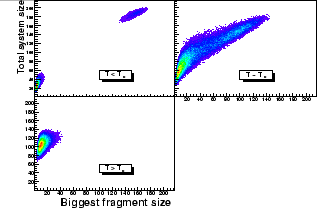
La figure (1) représente la distribution des évènements grand-canoniques (à la valeur critique du potentiel chimique $\mu = 3\epsilon$) dans l'espace ``taille totale du système (ie. densité) versus taille du plus gros fragment'' et montre la corrélation entre ces deux observables. Cette figure montre que même en système de toute petite taille la coéxistence de phase est reconnaissable par la bimodalité de la distribution du paramètre d'ordre. La claire corrélation entre $A_{big}$ et et la masse totale du système $A_{tot}$ démontre en plus que $A_{big}$ peut être utilisé comme paramètre d'ordre. Cette observable est facile à manipuler dans les simulations numériques et accessible assez facilement expérimentalement. La densité étant beaucoup plus difficile (voire impossible du fait de la difficulté d'accéder au volume) à mesurer, l'étude de cette observable est d'un grand interêt pour faire des analogies ou comparer les résultats des modèles avec l'expérience.

Figure 1: Densité de probabilité grand-canonique projetée dans l'espace ``nombre total de fragments'' (ordonnées) versus ``taille du plus gros fragment'' (abscisse) pour différentes températures (dans un réseau 6x6x6)

A basse température la distribution de ces observables est bimodale (la projection sur chaque axe révèle deux maxima). Les évènements denses (grande masse totale) et ayant un gros plus gros fragment $A_{big}$ sont identifiés comme appartenant à la phase de type liquide tandis que le deuxième lot d'évènements (faible densité et petite taille du plus gros fragment) correspond à la phase gazeuse. En élevant progressivement la température du système, ces deux lots d'évènements se rapprochent l'un de l'autre pour fusionner à la température critique. Enfin pour les températures surcritiques la distribution devient monomodale (un maximum), une seule phase fluide subsiste, avec un plus gros fragment de petite taille. Ainsi le passage d'une distribution bimodale à une distribution monomodale signe le passage par un point critique correspondant à la transition de phase du second ordre.

Figure 2: Distribution de taille du plus gros fragment pour différentes températures dans l'ensemble grand-canonique (haut) et dans l'ensemble canonique (bas).

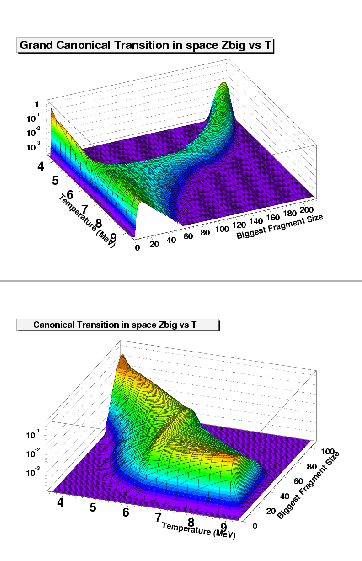La figure (2) (graphique supérieure) schématise la bifurcation caractéristique d'une transition de phase. Cette figure montre la distribution grand-canonique du plus gros fragment pour différentes températures. Le passage de la distribution bimodale de ce paramètre d'ordre à une distribution monomodale est bien localisée et permet d'identifier le point critique. Le graphique inférieur sur cette même figure présente les distributions du plus gros fragment dans la même gamme de températures pour l'ensemble canonique. Dans cet ensemble la masse a été fixée, c'est-à-dire le nombre de sites occupés est maintenu constant, alors qu'il était libre de fluctuer (sous la contrainte du potentiel chimique) dans l'ensemble grand-canonique. Si l'existence d'une loi de conservation empêche évidement l'utilisation de la masse totale comme paramètre d'ordre, la bimodalité de la distribution de taille du plus gros fragment a aussi disparu dans cet ensemble. La contrainte sur l'observable ``masse totale du système'' a fondamentalement changé la topologie de la distribution de $A_{big}$ à cause de la forte corrélation entre $A_{big}$ et $A_{tot}$. Le plus gros fragment n'est plus un paramètre d'ordre pour cet ensemble et ne permet plus de caractériser la coéxistence de phase.